What I mean by “dimension mapping” is representing a point in a space of N dimensions with a smaller number of dimensions. For example, what’s below shows a method of mapping a 2-D space with a single number.

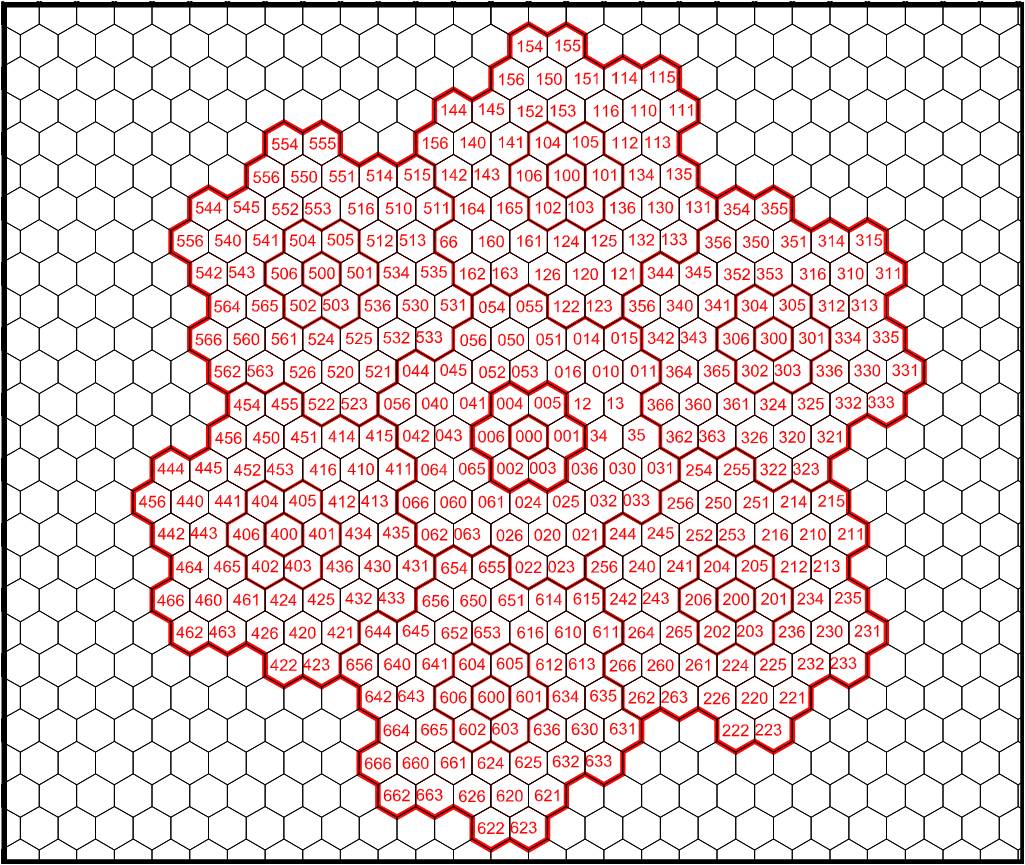
“Generalized Balanced Ternary” is a way to capture positional information for 2 dimensions using a single number (using digits 0-6) mapped onto hexagonal patterns. The web source for the following image is no longer around. A search (2023) for “generalized balanced ternary” led to this PDF on the topic.

The edges of the spaces change as one looks at finer or grosser detail. For instance, all the areas represented by “1xx” (1 and any following digits) is roughly a hexagon, but not quite. Likewise for the smaller groups, e.g., “10x” or “31x”. The corners that “matter” are the ones at digit transitions, e.g., where areas 123, 356, and 015 meet [I’ll use shorthand (123, 356, 015)]. A line from there to (162, 531, 054) separates “0xx” from “1xx”; from there to (362, 031, 254) separates “0xx” from “3xx”; from there to (undesignated, 131, 354) separates “1xx” from “3xx”. At the next level of detail, additional corners “matter”. Along the first pair, one would add the points (122,051,014) and (163, 126, 055).

I explored something quite similar decades ago. I think the Vector Equilibrium (VE) – or its space-filling dual, the rhombic dodecahedron – might be used to encode 3 dimensions in a single number (using digits with values 0-12) in a similar manner. It would be interesting to use a zero-centered notation for these values (digits -3 to 3 for hexagons, -6 to +6 for VE-based pattern).

In this light, Cartesian coordinates could be seen as a method for reducing the number of coordinates needed – e.g., to represent a point in 4M3, 6(0)M3, or 6(1)M3 using Cartesian 3M3 (see Dimensionalities for what 4M3, etc. mean).