Introduction

Number bases let one express large numbers as a series of smaller numbers, usually with the digits in decreasing levels of significance (…, 100’s, 10’s, 1’s, 1/10th’s, 1/100th’s, …). The number base limits the range of values a digit can take. In base ten we use the digits 0 to 9. A computer’s numbers are often expressed in binary (base 2), octal (base eight) or hexadecimal (base sixteen).

In all bases, each digit can range in value from 0 to 1 in base 2, 0 to 9 in base ten, 0 to 15 (0-9 and A [ten] to F [15]) in base sixteen. Used this way, the smallest value for a digit is zero, the largest is one less than the base number.

In odd numbered bases there’s another arrangement of digits one can use, called a balanced base, that has zero at the center and the same number of steps in value below and above zero. So in base 3, from -1 to +1; in base 5, from -2 to +2; in base 9, from -4 to +4. — each base 9 digit can also be expressed with two base 3 digits.

I first encountered the idea of balanced bases in college, reading Donald Knuth’s The Art of Computer Programming – relevant here, volume 2 (Seminumerical Algorithms). [The Positional Numbering Systems chapter is on the web. It contains both the quotes shown on this page (search “balanced” or “lalanne“).] On page 190 of the book he states:

Perhaps the prettiest number system of all is the balanced ternary notation, which consists of base-3 representation using -1, 0, and +1 as “trits” (ternary digits) instead of 0, 1, and 2.

Donald Knuth, The Art of Computer Programming, volume 2 (Seminumerical Algorithms, 2nd ed. 1981)

On page 192 he discusses the history of the idea and its potential application in computer design.

The first true appearance of “pure” balanced ternary notation was in an article by Léon Lalanne …, who was a designer of mechanical devices for arithmetic. Thomas Fowler independently invented and constructed a balanced ternary calculator at about the same time …. The balanced ternary number system was mentioned only rarely for the next 100 years, until the development of the first electronic computers at the Moore School of Electrical Engineering in 1945-1946; at that time it was given serious consideration along with the binary system as a possible replacement for the decimal system. The complexity of arithmetic circuitry for balanced ternary arithmetic is not much greater than it is for the binary system, and a given number requires only ln 2 / ln 3 ~= 63% as many digit positions for its representation. … The experimental Russian computer SETUN was based on balanced ternary notation … perhaps the symmetric properties and simple arithmetic of this number system will prove to be quite important some day—when the “flip-flop” is replaced by a “flip-flap-flop”.

It seems to me that the material world would naturally “use” zero-centered arithmetic. Values are “on target” or to one side or the other.  For numbers expressed with a zero-centered set of digits, there is no difference between rounding and truncating a number. Only the odd-valued bases: 3, 5, 7, etc. can be balanced. In even-valued bases, there would need to be two zeroes (-0 and +0) or a negative or positive digit without a balancing digit of the opposite sign (e.g., -4 to +5 in base ten) and hence not quite balanced. Balanced ternary (using digits with values -1, 0, and +1) is the smallest balanced base.

Here are diagrams representing the “standard” (top) and balanced (bottom) versions of base 3. In both diagrams, the most significant digits appear at the top, the least significant at the bottom.

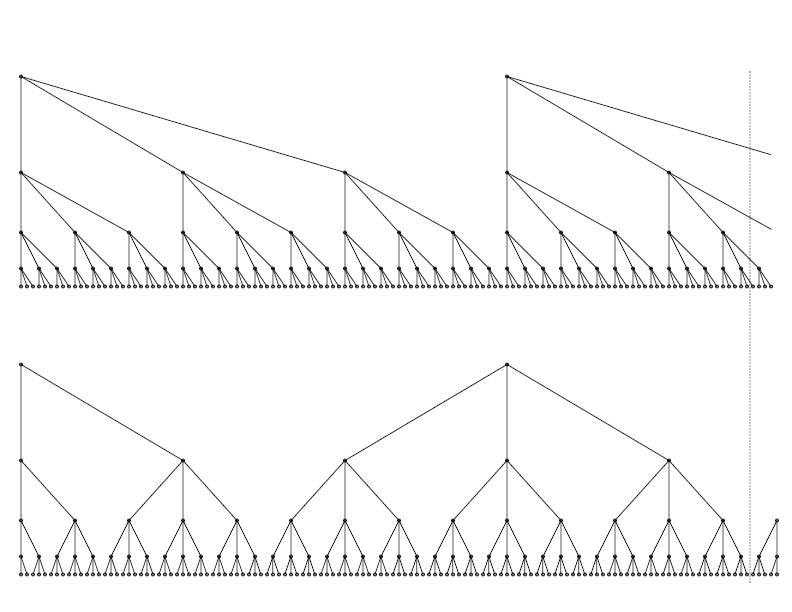
In the first form, the descending lines from a single point represent the digits 0, 1, or 2. In the second form, the descending lines represent the digits -1 (to the left), 0 (vertical), or 1 (to the right). Here’s how one would count from -5 to +13 in balanced base 3, using “<” for a digit with value -1, and “>” for a digit with value +1. In these three-digit numbers the first is the 9’s place, the second is the 3’s place, and the third is the 1’s place. So the first number in this sequence, <>> represents (-9)+(+3)+(+1) = -5.

The sequence: -5: <>> | -4: 0<< | -3: 0<0 | -2: 0<> | -1: 00< | zero: 000 | +1: 00> | +2: 0>< | +3: 0>0 | +4: 0>> | +5: ><< | +6: ><0 | +7 : ><> | +8: >0< | +9: >00 | +10: >0> | +11: >>< | +12: >>0 | +13: >>>.

Other Sources

A few years ago I ran into Abhijit Bhattacharjee of India via the web. He had a site that can still be found at http://replay.web.archive.org/20090312094241/http://abhijit.info/tristate/tristate.html with much more information on this idea. His extensive bibliography can be found at http://replay.web.archive.org/20090221122459/http://abhijit.info/tristate/biblio.htm .

As of this writing, you can find more on this topic at www.solbakkn.com/math. It also includes information on N-Grams, and a pointer to information (in a PDF file) on Dimensionalities, two other math topic of interest to me. Much of that information is now on this site’s pages and posts.

This page started out as a post still on this site’s blog. You can see some comments that were added there.